---

1. Understanding Packages and Libraries in VHDL

VHDL (VHSIC Hardware Description Language) is a powerful language used for modeling and simulating digital systems. One of the key features that makes VHDL versatile is its support for packages and libraries, which facilitate code reuse and modular design. In this article, we will explore the concepts of packages and libraries in VHDL, how to use standard packages, and how to create custom packages.

1.1 Packages

A package in VHDL is a collection of related declarations, such as types, subprograms (procedures and functions), constants, and components, that can be shared across multiple design units. Packages help in organizing and managing large VHDL designs by promoting code reuse and reducing redundancy.

1.2 Libraries

A library in VHDL is a logical collection of design units (entities, architectures, packages, and configurations). Libraries provide a way to organize and manage related design units, making it easier to locate and reference them in a project. Every VHDL design unit belongs to a library, with the default library being work.

2. Using Standard Packages

VHDL provides several standard packages that contain useful declarations for digital design. Some of the most commonly used standard packages are:

1. std_logic_1164: Defines the std_logic and std_ulogic types and associated logic operations.
2. numeric_std: Defines arithmetic operations for signed and unsigned types.
3. std_logic_arith: An older package that defines arithmetic operations for std_logic_vector.

To use these standard packages, you need to include them in your VHDL design using the use clause. Here is an example:

library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.numeric_std.all;

entity Example is
    Port ( a : in  std_logic_vector(7 downto 0);
           b : in  std_logic_vector(7 downto 0);
           sum : out std_logic_vector(7 downto 0));
end Example;

architecture Behavioral of Example is
begin
    process(a, b)
    variable a_int, b_int, sum_int : signed(7 downto 0);
    begin
        a_int := signed(a);
        b_int := signed(b);
        sum_int := a_int + b_int;
        sum <= std_logic_vector(sum_int);
    end process;
end Behavioral;

In this example, we use the std_logic_1164 and numeric_std packages from the IEEE library to define and manipulate std_logic_vector and signed types.

3. Creating Custom Packages

Creating custom packages in VHDL allows you to encapsulate and reuse your own declarations across multiple design units. Here is a step-by-step guide to creating and using a custom package:

• Define the Package: Create a new VHDL file for your package and define the package header and body.

-- my_package.vhdl
library IEEE;
use IEEE.std_logic_1164.all;

package my_package is
    constant MY_CONSTANT : integer := 0;
    type my_array is array (0 to 7) of std_logic;
    function my_function(a, b : integer) return integer;
end my_package;

package body my_package is
    function my_function(a, b : integer) return integer is
    begin
        return a + b;
    end my_function;
end my_package;

• Compile the Package: Before using the custom package in other design units, compile it using your VHDL compiler or simulation tool.

• Use the Package: Include the custom package in your VHDL design using the use clause.

library IEEE;
use IEEE.std_logic_1164.all;
use work.my_package.all;

entity CustomExample is
    Port ( a, b : in  integer;
           result : out integer);
end CustomExample;

architecture Behavioral of CustomExample is
begin
    process(a, b)
    begin
        result <= my_function(a, b) + MY_CONSTANT;
    end process;
end Behavioral;

• Test bench VHDL code

library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.numeric_std.all;
use work.my_package.all;

entity tb_custom_example is
-- No ports in a test bench entity
end tb_custom_example;

architecture testbench of tb_custom_example is
    -- Component declaration for the Unit Under Test (UUT)
    component custom_exemple
        Port ( a, b  : in  integer;
               result : out integer);
    end component;

    -- Signal declarations to connect to UUT
    signal a, b : integer := 0;
    signal result : integer;

begin
    -- Instantiate the Unit Under Test (UUT)
    uut: custom_exemple
        Port map (
            a => a,
            b => b,
            result => result
        );

    -- Stimulus process
    stim_proc: process
    begin
        -- Test case 1
        a <= 10;
        b <= 20;
        wait for 10 ns;

        -- Check result
        assert result = (my_function(10, 20) + MY_CONSTANT)
        report "Test case 1 failed" severity error;

        -- Test case 2
        a <= -5;
        b <= 15;
        wait for 10 ns;

        -- Check result
        assert result = (my_function(-5, 15) + MY_CONSTANT)
        report "Test case 2 failed" severity error;

        -- Add more test cases as needed

        -- End of test
        wait;
    end process;

end testbench;

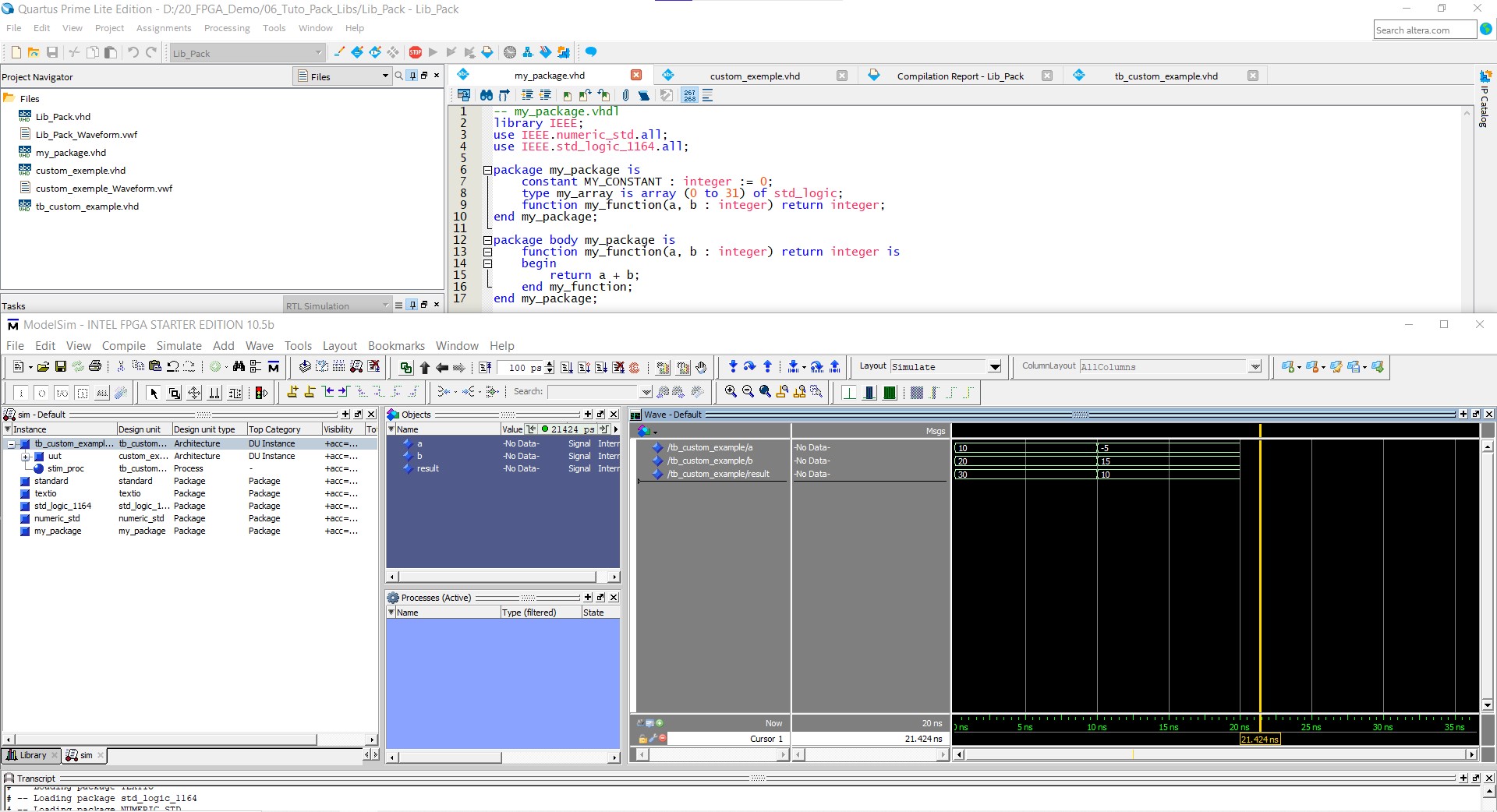
In this example, we define a custom package my_package that includes a constant, a type, and a function. We then use this package in an entity called CustomExample.

---

3. Multiplication Example Using Libraries and Binary Method in VHDL

Multiplication of binary numbers is a common operation in digital design, and VHDL provides various ways to implement it. One effective way is to use libraries, such as std_logic_1164 and numeric_std, along with the binary method of multiplication. In this example, we will implement a multiplier using these libraries and the binary method.

3.1 Define the Entity

First, we define the entity for our multiplier. This entity will have two input ports for the multiplicand and multiplier and one output port for the product.

library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.numeric_std.all;

entity BinaryMultiplier is
    Port (
        a : in std_logic_vector(7 downto 0);
        b : in std_logic_vector(7 downto 0);
        product : out std_logic_vector(15 downto 0)
    );
end BinaryMultiplier;

3.2 Implement the Architecture

Next, we implement the architecture for the multiplier. We use the binary method, also known as the shift-and-add method, to perform the multiplication.

library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.numeric_std.all;

entity BinaryMultiplier is
    Port (
        a : in std_logic_vector(7 downto 0);
        b : in std_logic_vector(7 downto 0);
        product : out std_logic_vector(15 downto 0)
    );
end BinaryMultiplier;

architecture Behavioral of BinaryMultiplier is
begin
    process(a, b)
        variable multiplicand : unsigned(7 downto 0);
        variable multiplier : unsigned(7 downto 0);
        variable result : unsigned(15 downto 0);
        variable temp : unsigned(15 downto 0); -- Temporary variable for shifting
    begin
        multiplicand := unsigned(a);
        multiplier := unsigned(b);
        result := (others => '0');

        -- Binary multiplication using shift-and-add method
        for i in 0 to 7 loop
            if multiplier(0) = '1' then
                temp := unsigned(resize(multiplicand, 16)); -- Resize multiplicand to 16 bits
                result := result + temp;
            end if;
            multiplicand := multiplicand sll 1;
            multiplier := multiplier srl 1;
        end loop;

        product <= std_logic_vector(result);
    end process;
end Behavioral;

3.3 Explanation

In this architecture:

• We use the unsigned type from the numeric_std package for arithmetic operations.
• We initialize result to zero.
• We loop through each bit of the multiplier.
• If the least significant bit (LSB) of the multiplier is 1, we add the multiplicand to the result.
• We shift the multiplicand left (logical shift) and the multiplier right (logical shift) in each iteration.
• Finally, we assign the result to the product output.

3.4 Testbench

To verify the functionality of our multiplier, we create a testbench.

library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.numeric_std.all;

entity Testbench is
end Testbench;

architecture Behavioral of Testbench is
    signal a, b : std_logic_vector(7 downto 0);
    signal product : std_logic_vector(15 downto 0);

    component BinaryMultiplier
        Port (
            a : in std_logic_vector(7 downto 0);
            b : in std_logic_vector(7 downto 0);
            product : out std_logic_vector(15 downto 0)
        );
    end component;
begin
    uut: BinaryMultiplier port map (a => a, b => b, product => product);

    process
    begin
        a <= "00000011";  -- 3 in binary
        b <= "00000101";  -- 5 in binary
        wait for 10 ns;
        assert (product = "0000000000001111") report "Test failed!" severity error;

        a <= "00000110";  -- 6 in binary
        b <= "00000010";  -- 2 in binary
        wait for 10 ns;
        assert (product = "0000000000001100") report "Test failed!" severity error;

        a <= "00001111";  -- 15 in binary
        b <= "00001111";  -- 15 in binary
        wait for 10 ns;
        assert (product = "0000000011100001") report "Test failed!" severity error;

        wait;
    end process;
end Behavioral;

---

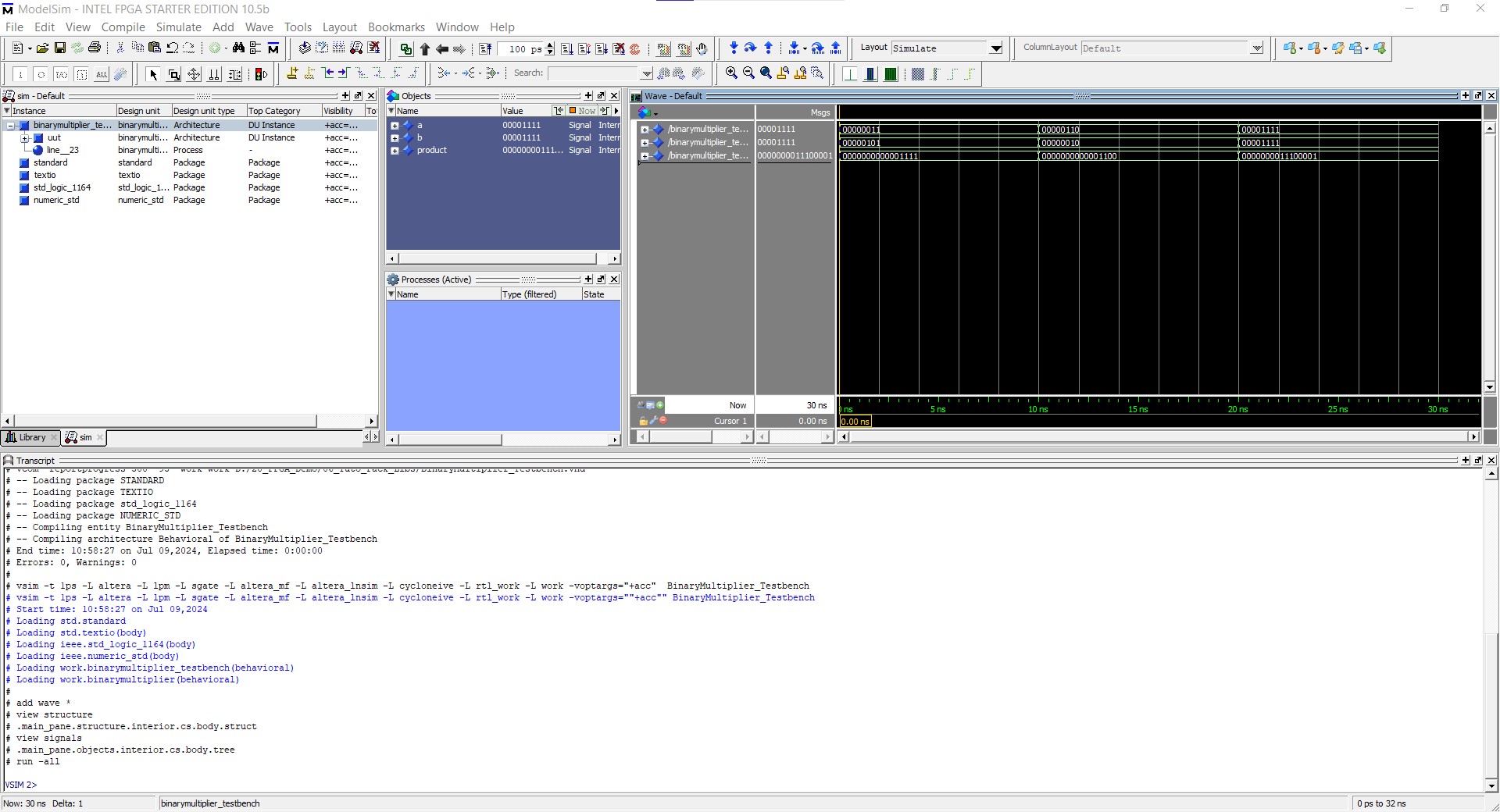
4. Using a very fast Architecture (without process)

To implement a fast binary multiplier using logical gates and one-bit multipliers in VHDL, you can use a combinational approach based on partial products and adders. This method involves creating a matrix of partial products and summing them using adders.

We could establish a multiplication unit utilizing an array of full adders and AND gates. The following image illustrates the concept of binary multiplication:

This architecture come form the following formula:

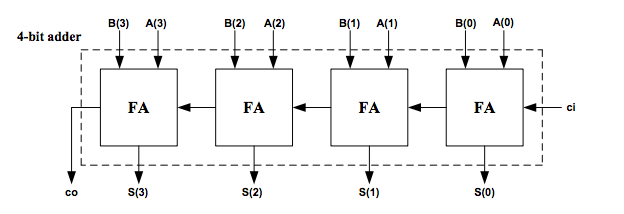
TTo simplify things, we could define a sequence of four full adders to make the design more compact and clearer:

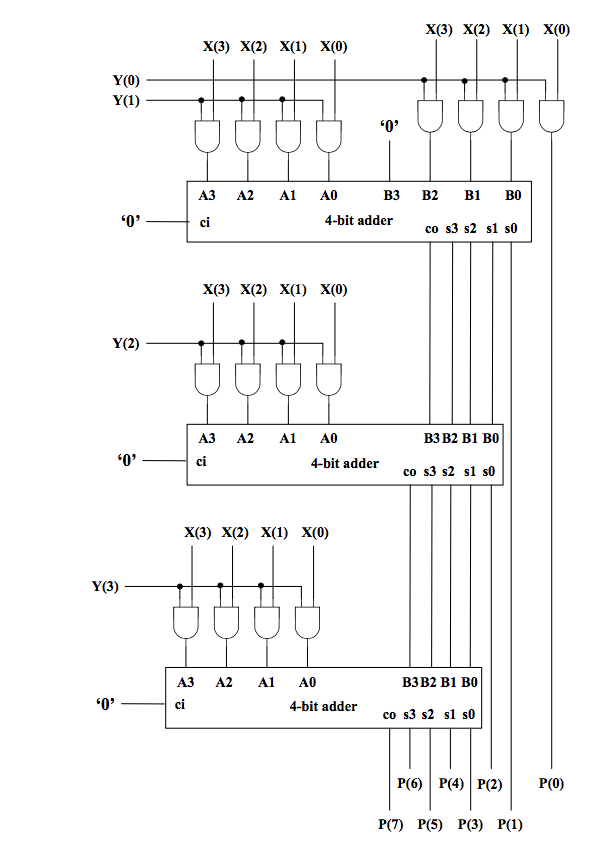
With the new 4-bit full adder, the 4-bit multiplier can be represented as follows:

4.1 Define One-Bit Multiplier

A one-bit multiplier is essentially an AND gate. When multiplying two bits, the result is 1 if both bits are 1, otherwise it is 0.

library IEEE;
use IEEE.std_logic_1164.all;

entity OneBitMultiplier is
    Port (
        a : in std_logic;
        b : in std_logic;
        product : out std_logic
    );
end OneBitMultiplier;

architecture Behavioral of OneBitMultiplier is
begin
    product <= a and b;
end Behavioral;

4.2 Define Half Adder and Full Adder

Next, you need to define the half adder and full adder components to sum the partial products.

4.2.1 Half Adder

The half adder come from the following expression: S = a XOR b, C = a * b

library IEEE;
use IEEE.std_logic_1164.all;

entity HalfAdder is
    Port (
        a : in std_logic;
        b : in std_logic;
        sum : out std_logic;
        carry : out std_logic
    );
end HalfAdder;

architecture Behavioral of HalfAdder is
begin
    sum <= a xor b;
    carry <= a and b;
end Behavioral;

4.2.2 Full Adder

The full adder come from the following expression: Cout = a * b + Cin * ( a XOR b ), Sum = a XOR b XOR Cin

library IEEE;
use IEEE.std_logic_1164.all;

entity FullAdder is
    Port (
        a : in std_logic;
        b : in std_logic;
        cin : in std_logic;
        sum : out std_logic;
        cout : out std_logic
    );
end FullAdder;

architecture Behavioral of FullAdder is
begin
    sum <= a xor b xor cin;
    cout <= (a and b) or (cin and (a xor b));
end Behavioral;

4.2.3 4bit full adder

Based on the full adder already defined, we could define the following 4-bit full adder.

library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.numeric_std.all;

entity Ripple_Adder is
    Port (
        A    : in  STD_LOGIC_VECTOR (3 downto 0);
        B    : in  STD_LOGIC_VECTOR (3 downto 0);
        Cin  : in  STD_LOGIC;
        S    : out STD_LOGIC_VECTOR (3 downto 0);
        Cout : out STD_LOGIC
    );
end Ripple_Adder;

architecture Behavioral of Ripple_Adder is

    -- Full Adder VHDL Code Component Declaration
    component Fulladder
        Port (
            a    : in  std_logic;
            b    : in  std_logic;
            cin  : in  std_logic;
            sum  : out std_logic;
            cout : out std_logic
        );
    end component;

    -- Intermediate Carry declaration
    signal c1, c2, c3 : STD_LOGIC;

begin

    -- Port Mapping Full Adder 4 times
    FA1: Fulladder port map(
        a    => A(0),
        b    => B(0),
        cin  => Cin,
        sum  => S(0),
        cout => c1
    );

    FA2: Fulladder port map(
        a    => A(1),
        b    => B(1),
        cin  => c1,
        sum  => S(1),
        cout => c2
    );

    FA3: Fulladder port map(
        a    => A(2),
        b    => B(2),
        cin  => c2,
        sum  => S(2),
        cout => c3
    );

    FA4: Fulladder port map(
        a    => A(3),
        b    => B(3),
        cin  => c3,
        sum  => S(3),
        cout => Cout
    );

end Behavioral;

4.3 Define the 4-Bit Multiplier

Now, you can create the 4-bit multiplier using the one-bit multipliers, half adders, and full adders.

library ieee;
use ieee.std_logic_1164.all;
-- use ieee.std_logic_textio.all;   -- NOT USED
-- use ieee.std_logic_unsigned.all; -- NOT USED

entity multy is 
    port (
        x: in  std_logic_vector (3 downto 0);
        y: in  std_logic_vector (3 downto 0);
        p: out std_logic_vector (7 downto 0)
    );
end entity multy;

architecture rtl of multy is
    component Ripple_Adder
        port ( 
            A:      in  std_logic_vector (3 downto 0);
            B:      in  std_logic_vector (3 downto 0);
            Cin:    in  std_logic;
            S:      out std_logic_vector (3 downto 0);
           Cout:    out std_logic
        );
    end component;
-- AND Product terms:
    signal G0, G1, G2:  std_logic_vector (3 downto 0);
-- B Inputs (B0 has three bits of AND product)
    signal B0, B1, B2:  std_logic_vector (3 downto 0);

begin

    -- y(1) thru y (3) AND products, assigned aggregates:
    G0 <= (x(3) and y(1), x(2) and y(1), x(1) and y(1), x(0) and y(1));
    G1 <= (x(3) and y(2), x(2) and y(2), x(1) and y(2), x(0) and y(2));
    G2 <= (x(3) and y(3), x(2) and y(3), x(1) and y(3), x(0) and y(3));
    -- y(0) AND products (and y0(3) '0'):
    B0 <=  ('0',          x(3) and y(0), x(2) and y(0), x(1) and y(0));

-- named association:
cell_1: 
    Ripple_Adder 
        port map (
            a => G0,
            b => B0,
            cin => '0',
            cout => B1(3), -- named association can be in any order
            S(3) => B1(2), -- individual elements of S, all are associated
            S(2) => B1(1), -- all formal members must be provide contiguously
            S(1) => B1(0),
            S(0) => p(1)
        );
cell_2: 
    Ripple_Adder 
        port map (
            a => G1,
            b => B1,
            cin => '0',
            cout => B2(3),
            S(3) => B2(2),
            S(2) => B2(1),
            S(1) => B2(0),
            S(0) => p(2)
        );
cell_3: 
    Ripple_Adder 
        port map (
            a => G2,
            b => B2,
            cin => '0',
            cout => p(7),
            S => p(6 downto 3)  -- matching elements for formal
        );
    p(0) <= x(0) and y(0); 
end architecture rtl;

• Test on waveforme simulator

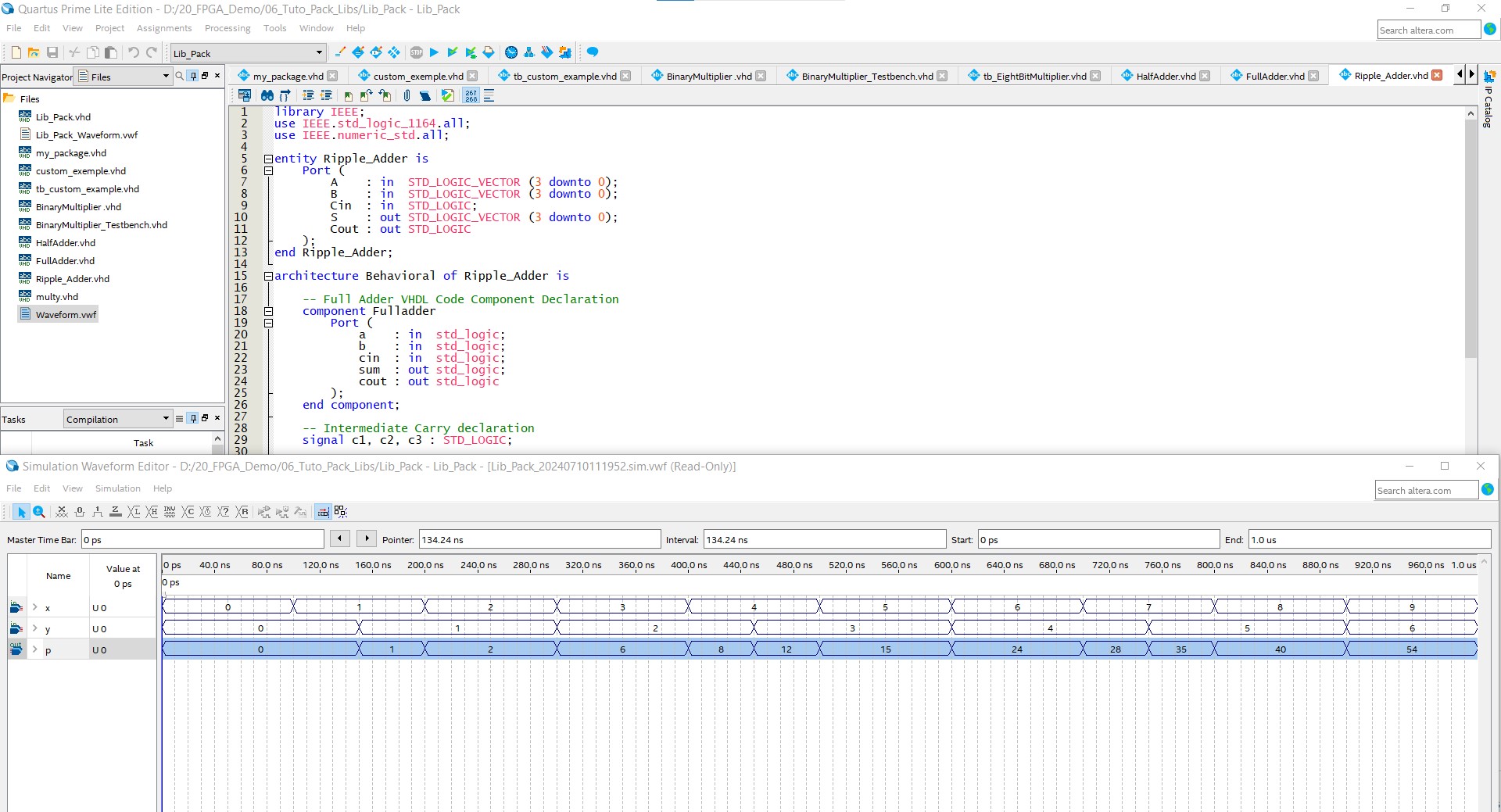
5. Conclusion

This example demonstrates how to implement an 4-bit multiplier in VHDL using one-bit multipliers, half adders, and full adders for a purely combinational and high-speed design. Leveraging the std_logic_1164 and numeric_std libraries, the binary method (shift-and-add) is employed for efficient multiplication. The testbench verifies the multiplier's correctness. Utilizing packages and libraries in VHDL simplifies the design process, promotes modularity, and enhances productivity and maintainability.

📝 Article Author : SEMRADE Tarik
🏷️ Author position : Embedded Software Engineer
🔗 Author LinkedIn : LinkedIn profile